Practical Quantum Neural Network Computation on Noisy, Intermediate Scale-Quantum Computers

Practical Quantum Neural Network Computation on Noisy, Intermediate Scale-Quantum Computers

PI of the project: Prof. Ahmed Hazem El-Mahdy

Funded by:

• STDF
• E-JUST
• Waseda

Highlights:

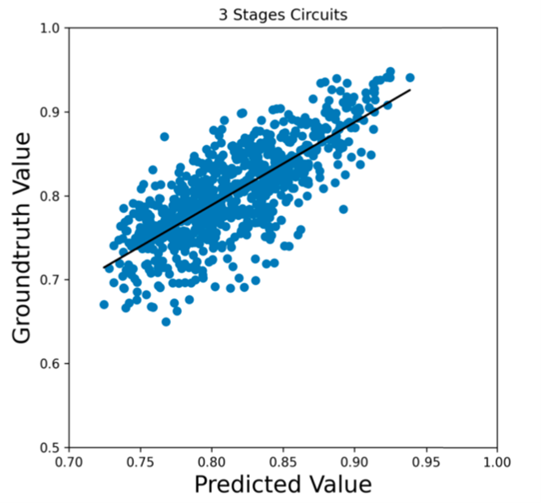
Fidelity Estimation:

• Estimating the Fidelity is a very complex task, requiring an exponential number of experiments
• We showed that we can learn the fidelity using CNN with  polynomial complexity

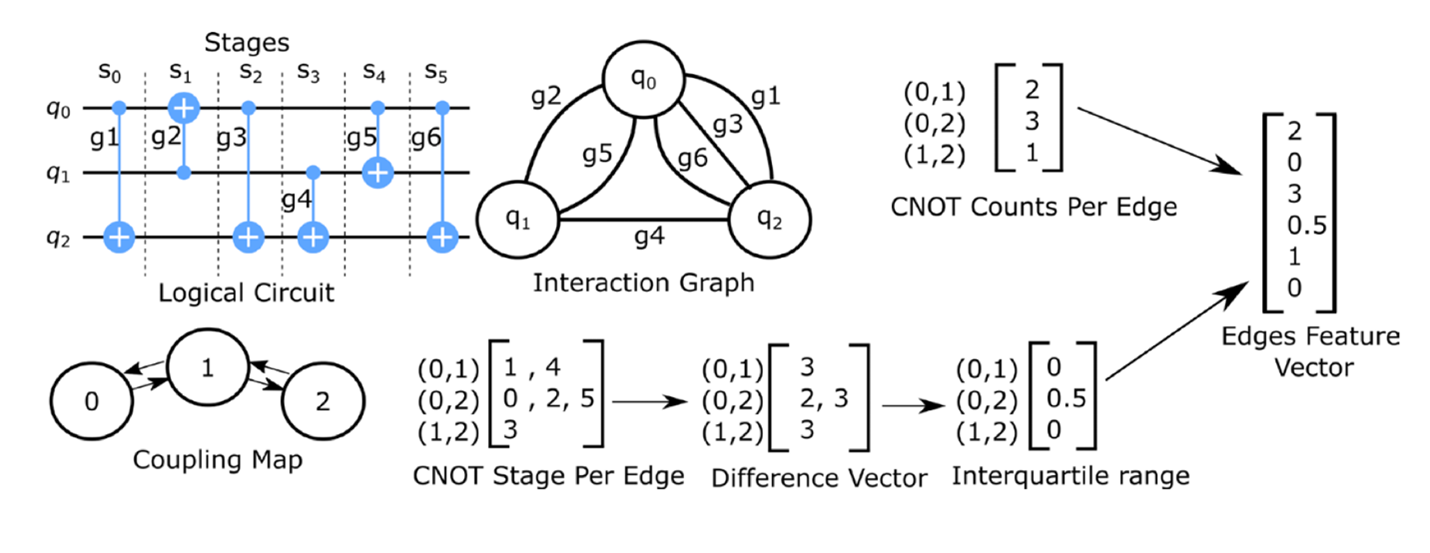
Improving Fidelity:

• The way quantum circuits are mapped into physical qubits significantly affects their fidelity
• We used reinforcement learning to reach a ‘good’ map
• We are comparable by the state-of-the-art but our approach is much faster:
• More than 10 times reduction on the feature-length size!

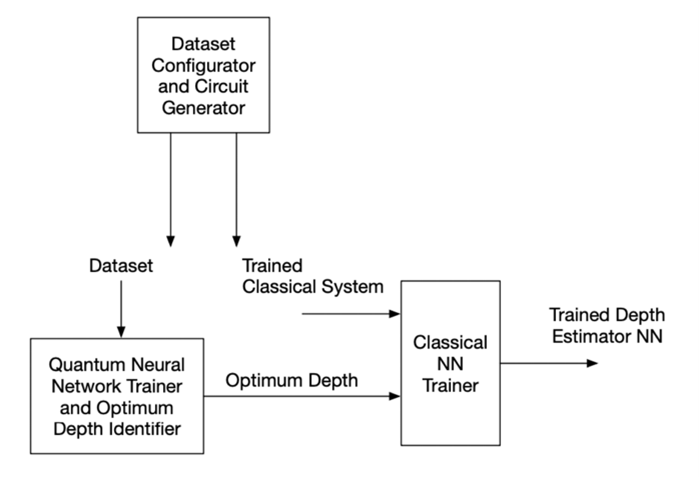
Circuit Parameterisation for Quantum Machine Learning:

• QNN dramatically reduces the number of parameters compared to classical
• An important issue is the number of parameters, need to avoid:
  • Overparameterisation
  • Underparameterisation
• We estimate the number of layers in the QNN given a standard NN
• We achieve 86.7% accuracy